Chào mừng quý vị đến với TOÁN THPT - PHẠM KIM CHUNG.
Hệ Phương Trình
1) $$\left\{ \begin{matrix} & x+y=2 \\ & {{x}^{3}}+{{y}^{3}}=26 \\
\end{matrix} \right.\left\{ \begin{matrix} & x\sqrt{y}+y\sqrt{x}=30 \\ &
x\sqrt{x}+y\sqrt{y}=35 \\ \end{matrix} \right.$$
3) $$\left\{ \begin{matrix} & \sqrt{x+\frac{1}{y}}+\sqrt{x+y-3}=3 \\ &
2x+y+\frac{1}{y}=8 \\ \end{matrix} \right.\left\{ \begin{matrix} & x+y+z=1 \\ & 2x+2y-2xy+{{z}^{2}}=1 \\
\end{matrix} \right.$$
5) $$\left\{ \begin{matrix} & {{x}^{3}}=2x+y \\ & {{y}^{3}}=2y+x \\
\end{matrix} \right.\left\{ \begin{matrix} & {{x}^{2}}-2{{y}^{2}}=2x+y \\ &
{{y}^{2}}-2{{x}^{2}}=2y+x \\ \end{matrix} \right.$$
7) $$\left\{ \begin{matrix} & \sqrt{x}+\sqrt{2-y}=\sqrt{2} \\ &
\sqrt{y}+\sqrt{2-x}=\sqrt{2} \\ \end{matrix} \right.\left\{ \begin{matrix} & 3{{x}^{2}}+2xy+{{y}^{2}}=11 \\ &
{{x}^{2}}+2xy+3{{y}^{2}}=17 \\ \end{matrix} \right.$$
9) $$\left\{ \begin{matrix} & {{x}^{2}}+{{y}^{2}}=5-2xy \\ & y\left( x+y
\right)=10 \\ \end{matrix} \right.\left\{ \begin{matrix} & 2{{x}^{2}}+{{y}^{2}}+3xy=12 \\ & 2{{\left(
x+y \right)}^{2}}-{{y}^{2}}=14 \\ \end{matrix} \right.$$
11) $$\left\{ \begin{matrix} & xy+x-y=-1 \\ & {{x}^{2}}+{{y}^{2}}-x+y=2 \\
\end{matrix} \right.\left\{ \begin{matrix} & {{x}^{2}}+xy+{{y}^{2}}-x+y=6 \\ & xy-x+y=-3
\\ \end{matrix} \right.$$
13) $$\left\{ \begin{matrix} & x\sqrt{y}+y\sqrt{x}=6 \\ &
{{x}^{2}}y+{{y}^{2}}x=20 \\ \end{matrix} \right.\left\{ \begin{matrix} & \sqrt{x}+\sqrt{y}=3 \\ &
\sqrt{x+5}+\sqrt{y+3}=5 \\ \end{matrix} \right.$$
15) $$\left\{ \begin{matrix} & {{x}^{3}}-\sqrt{y}=1 \\ &
5{{x}^{6}}-8{{x}^{3}}\sqrt{y}+2y=2 \\ \end{matrix} \right.\left\{ \begin{matrix} & x+\sqrt{1-{{y}^{2}}}=1 \\ &
y+\sqrt{1-{{x}^{2}}}=\sqrt{3} \\ \end{matrix} \right.$$.
Nguyễn Văn Năm @ 09:40 01/06/2009
Số lượt xem: 5401
- tìm hai số x, y (01/06/09)
- Phương trình chứa tham số . (22/05/09)
- Hệ phương trình - Luyện thi ĐH (14/05/09)
- Mọi ngươi thư giai bài BDT này xem (27/04/09)
- PT-BPT (19/04/09)
Bài 1
HPT$$\Leftrightarrow \left\{\begin{matrix} y=2-x\\x^{3}+\left(2-x \right)^{3}=26 \end{matrix}\right. $$
$$\Leftrightarrow \left\{\begin{matrix} y=2-x\\x^{2}-2x-3=0 \end{matrix}\right. $$
$$\Leftrightarrow \left(x;y \right)=\left(-1;3 \right),\left(3;-1 \right) $$
Em xin giải Bài 5
Đặt
Khi đó HPT

chia hai vế của hpt cho nhau ta được:
hoặc


hoặc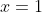


hoặc

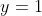
Vậy hpt có các No
Thêm Bài 13, mong Thầy mau khỏe
ĐK:
Đặt : ĐK:
ĐK: 
HPT đã cho

Ta có

Tiếp bài 2
$$HPT\Leftrightarrow \left\{\begin{matrix} \sqrt{x}\sqrt{y}\left(\sqrt{x}+\sqrt{y} \right)=30\\\left(x+y \right)\left(\sqrt{x}+\sqrt{y} \right)=65 \end{matrix}\right. $$
Đặt: $$\left\{\begin{matrix} \sqrt{x}+\sqrt{y}=a\\\sqrt{x}\sqrt{y}=b \end{matrix}\right. $$
Khi đó:
$$HPT\Leftrightarrow \left\{\begin{matrix} ab=30\\\left(a^{2}-2b \right)a=65 \end{matrix}\right. $$
Giải ra: $$\left\{\begin{matrix} a=5\\b=6 \end{matrix}\right. $$
Bài 11
Đặt: $$\left\{\begin{matrix} a=x-y\\b=xy \end{matrix}\right. $$
$$HPT\Leftrightarrow \left\{\begin{matrix} a+b=-1\\a^{2}+2b-a-2=0 \end{matrix}\right. $$
$$\Leftrightarrow \left(a;b \right)=\left(4;-5 \right),\left(-1;0 \right) $$
Giải ra:
Bài 12
Đặt: $$\left\{\begin{matrix} a=x-y\\b=xy \end{matrix}\right. $$
Khi đó:
$$HPT\Leftrightarrow \left\{\begin{matrix} a^{2}+3b-a=6\\b-a=-3 \end{matrix}\right. $$
$$\Leftrightarrow \left(a,b \right)=\left(3;0 \right),\left(-5;-8 \right) $$
Giải ra:
Vậy thì em cũng xin góp thêm bài 6
Thế vào hệ ta được:
Em xin giải bài 9:
$$HPT\Leftrightarrow \left\{\begin{matrix} (x+y)^{2}=5\\ y(x+y)=10 \end{matrix}\right.$$.
* .Giải ra ta được:
.Giải ra ta được:=(-\sqrt{5};2\sqrt{5})) .
.
*
 phương trình vô nghiệm.
phương trình vô nghiệm.